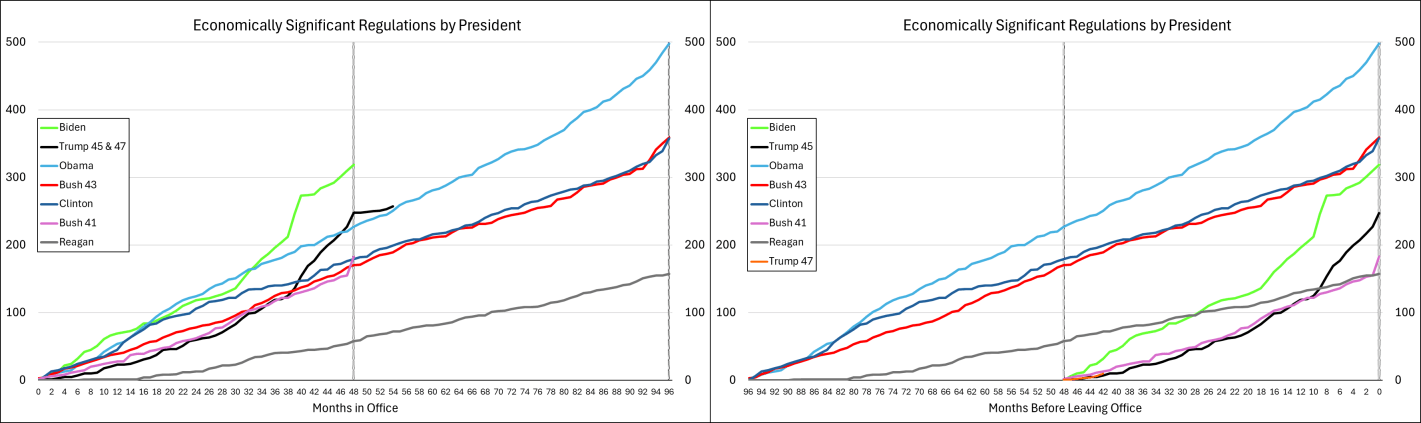
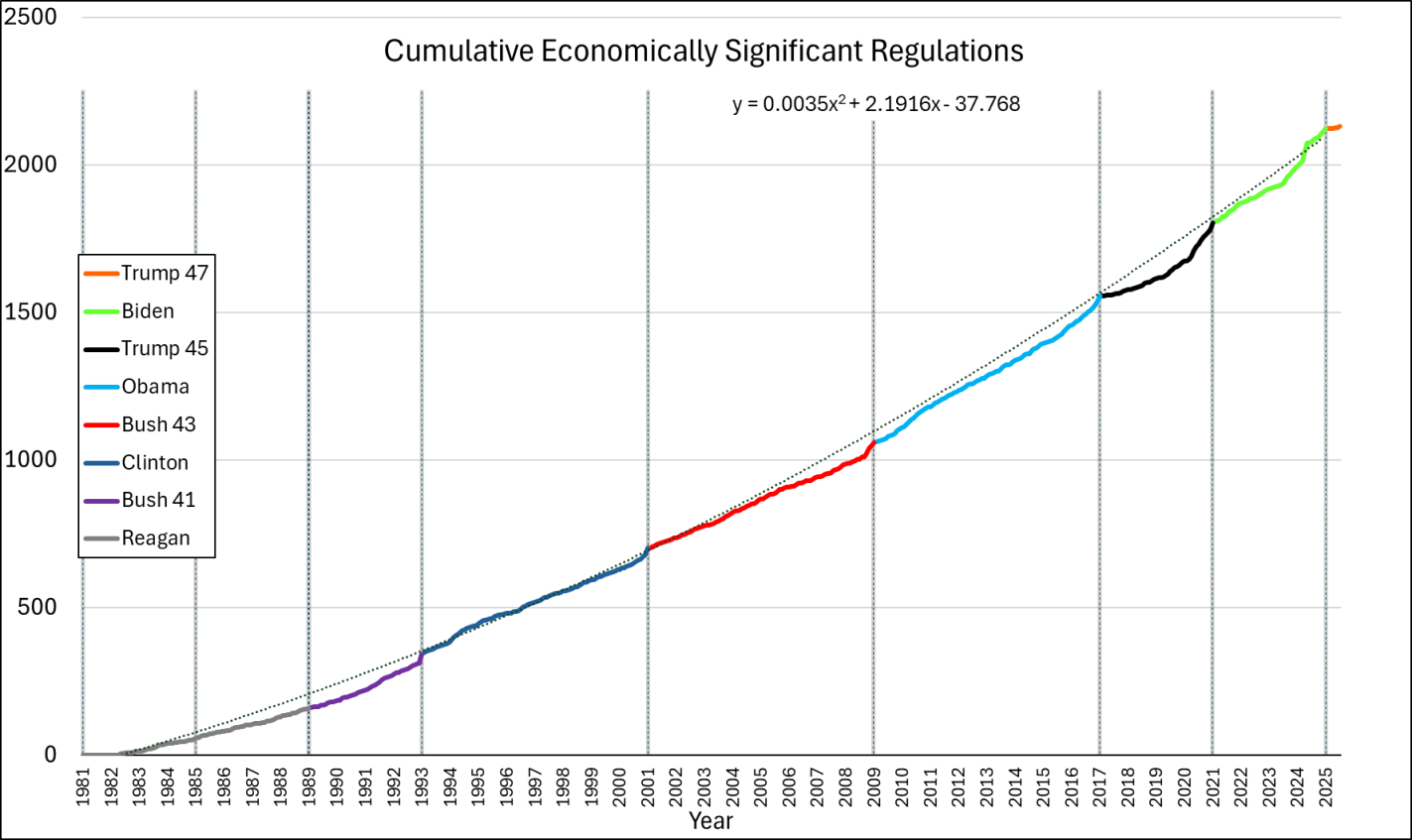
There are several requirements for Ricardian Equivalence:
- Individuals or their families act as infinitely lived agents.
- All governments and agents can borrow and lend at a single rate.
- The path of government expenditures is independent of financing choices
Assumption 2) appears patently absurd on its face. I certainly cannot borrow at the same interest rate that the US Treasury can. QED. Do not pass go, do not collect $200. The yield on 1-year US treasuries is 3.58%. I can’t borrow at that rate… Or can I?
Let’s do some casuistry.
What is a loan?
It’s a contract that:
- Provides the borrower with access to spending
- with or without collateral
- with a promise to repay the lender at defined times, usually with interest.
So, when you borrow $5 from a friend and pay it back on the same day, it’s a loan. The contract is verbal, there is no collateral, the repayment time is ‘soon’ with flexibility, and the interest rate is zero.
A mortgage is a collateralized loan. You borrow from a bank, make monthly payments for the term of the loan, and accrue interest on the principal. The contract is written, the house or a portion of its value is the collateral, and the interest rate is positive.
What about a Pawnshop loan? Most of us are probably unfamiliar with these. In this circumstance, a person has valuable non-assets that and the pawnshop has money. They engage in a contractual asset swap. The borrower lends the non-money asset to the pawnshop as collateral and borrows money from the pawnshop. The pawnshop borrows the non-money asset and lends the money to the borrower. The borrower can use the money as they please, but the pawnshop can not use the non-money asset – they can simply hold it. They collect interest in order to cover their opportunity costs.
One outcome is that the borrower repays the loan and interest by the maturity date and reclaims their non-money asset. Another outcome is that the borrower retains the option to default without any further obligation. But they lose the right to reclaim their property according to the repayment terms. If the borrower exercises the option to default, then the pawnshop acquires full rights to the non-money asset. The pawnshop often resells the asset at a profit. The profit is relatively reliable because the illiquidity of the non-money asset allows the pawnshop to lend much less than its retail value. That illiquidity is also why the borrower is willing to accept the terms.
If we accept that the pawnshop contract is a loan, which is just a collateralized loan with a mostly standard default option, then get ready for this.
Continue reading