Zachary Bartsch

From Cubicles to Code – Evolving Investment Priorities from 1990 to 2022

July 12, 2024July 13, 2024Zachary BartschLeave a comment

I’ve written before about how we can afford about 50% more consumption now that we could in 1990. But it’s not all bread and circuses. We can also afford more capital. In fact, adding to our capital stock helps us produce the abundant consumption that we enjoy today. In order to explore this idea I’m using the BEA Saving and Investment accounts. The population data is from FRED.

The tricky thing about investment spending is that we need to differentiate between gross investment and net investment. Gross investment includes spending on the maintenance of current capital. Net investment is the change in the capital stock after depreciation – it’s investment in additional capital not just new capital. Below are two pie charts that illustrate how the composition of our *gross investment* spending has changed over the past 30 years. Residential investment costs us about the same proportion of our investment budget as it did historically. A smaller proportion of our investment budget is going toward commercial structures and equipment (I’ve omitted the change in inventories). The big mover is the proportion of our investment that goes toward intellectual property, which has almost doubled.

It’s easiest for us to think about the quantities of investment that we can afford in 2022 as a proportion of 1990. Below are the inflation-adjusted quantities of investment per capita. On a per-person basis, we invest more in all capital types in 2022 than we did in 1990. Intellectual property investment has risen more than 600% over the past 30 years. The investment that produces the most value has moved toward digital products, including software. We also invest 250% more in equipment per person than we did in 1990. The average worker has far more productive tools at their disposal – both physical and digital. Overall real private investment is 3.5 times higher than it was 30 years ago.

Continue reading →

Market Preserving Federalism in the USA

July 5, 2024July 5, 2024Zachary Bartsch3 Comments

One of my favorite economic journal articles is by Barry Weingast and has the short title “Market Preserving Federalism” (MPF). In this paper, Weingast lays out the conditions necessary for two tenuous equilibria: A) Federalism & B) Federalism that preserves a market economy. Given that we just celebrated Independence Day in the USA, it seems to me like a good opportunity to share some brief thoughts on this paper. I’ll speak in terms of the US for ease.

Weingast enumerates 5 features for MPF, starting with two that characterize a stable federalism:

F1) A hierarchy of governments, that is, at least “two levels of governments rule the same land and people,” each with a delineated scope of authority so that each level of government is autonomous in its own, well-defined sphere of political authority

F2) The autonomy of each government is institutionalized in a manner that makes federalism’s restrictions self-enforcing

Continue reading →

Not Just Consumer Prices

June 28, 2024June 26, 2024Zachary BartschLeave a comment

We all know about inflation. One popular measure is the Consumer Price Index (CPI), which measures the change in price of a fixed basket of goods. The other popular measure used for inflation is the Personal Consumption Expenditures (PCE) price index. This index measures the price of what consumers actually purchase and captures the effects of consumers changing their consumption bundles over time. While the latter is a better measure for the prices at which consumers make purchases, it takes longer to calculate. In practice, the earlier CPI release gives a pretty accurate preview to the PCE price index.

While consumption is a substantial two-thirds of total expenditures in the US economy, other prices definitely matter. On average, a third of our income is spent on other things. Below is a stacked bar chart of quarterly GDP components – the classic Y=C+I+G+NX.* Investment spending composes a relatively stable 16.7% and Government spending composes about 16.5% of GDP. We almost never hear much about the price of these other things.

Continue reading →

Advice For Travelling With Children

June 21, 2024June 24, 2024Zachary Bartsch3 Comments

My family regularly takes long trips up and down the east coast of the US. It takes us about 6 hours just to travel through Florida. We have several kids between the ages of 1 & 7 and we’ve got it down to a pretty good science. Here’s some great advice for travelling with children. A lot of it is OK advice if you cherry pick, but together their benefits compound.

1) Depart Early

It doesn’t matter if it’s a 3 hour trip or a two day trip. To us, ‘early’ means that our target departure time is 5 AM, but ‘early’ may mean something different for you and yours. Benefits include:

Kids may remain or resume sleeping for the first portion of the travel. That’s time that they are occupied.
Earlier arrival at your destination gives kids time to burn off some energy and adults time to decompress. For multi-day trips, we like to stop at a hotel that has a pool.

2) Carry-on Backpacks

Just as you would have a small personal item on an airplane, such as a purse, give each child a backpack that contains car-ride content (make sure that they put away one thing before beginning the next). Maybe ensure that each kid has a different color. This puts their stimulation in their own hands. The idea is not to avoid interacting with your kids. The idea is to help them take care of themselves. Here’s what to include:

Continue reading →

Future Consumption Has Never Been Cheaper

June 14, 2024Zachary Bartsch1 Comment

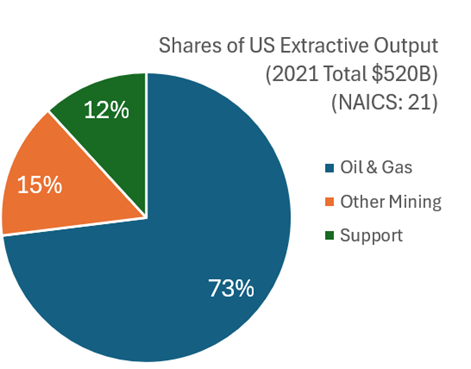
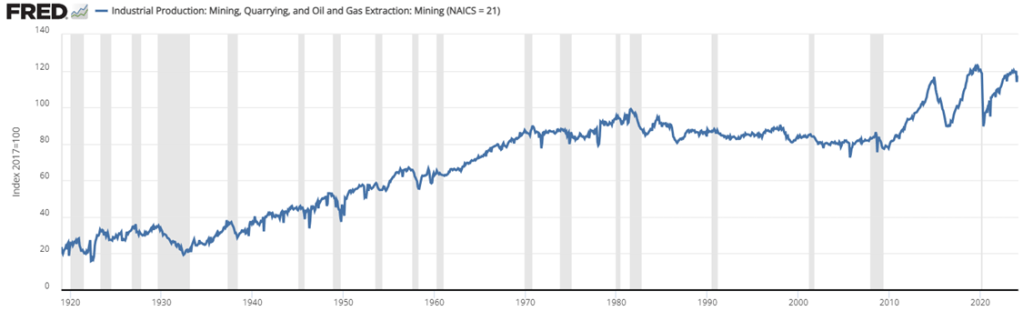
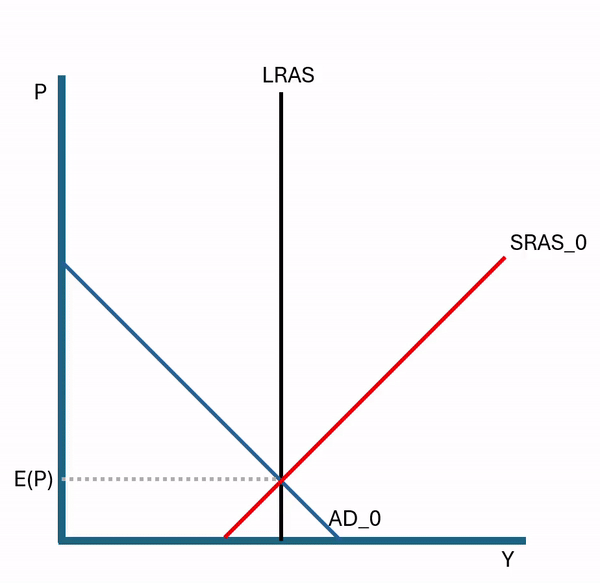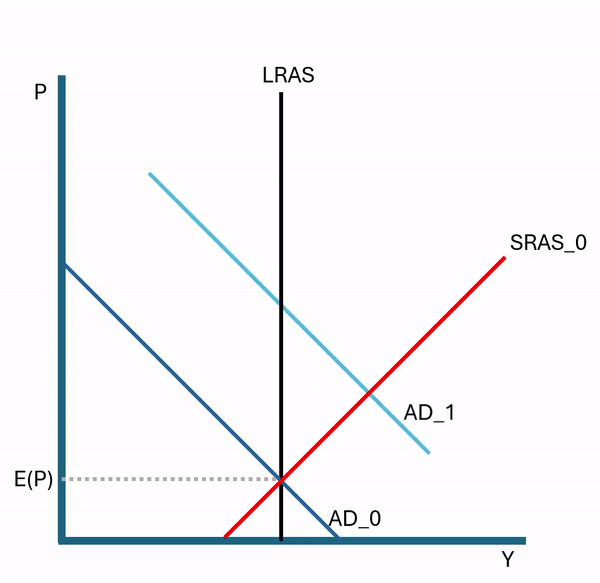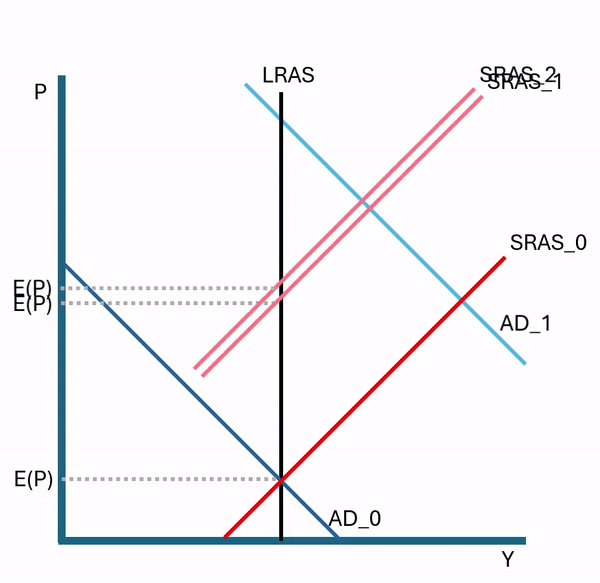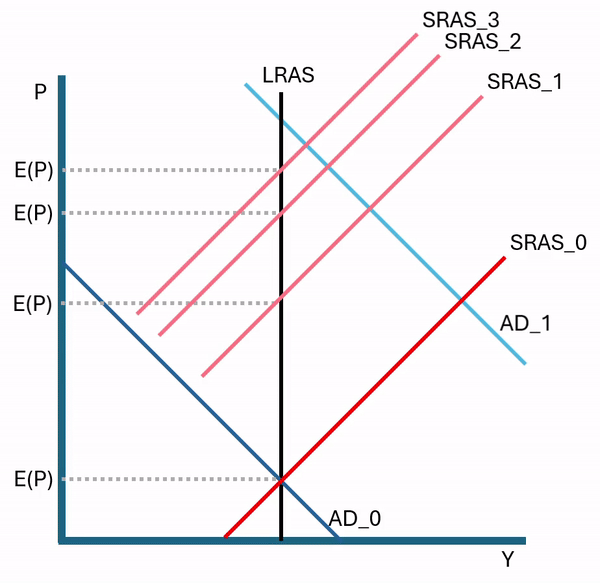
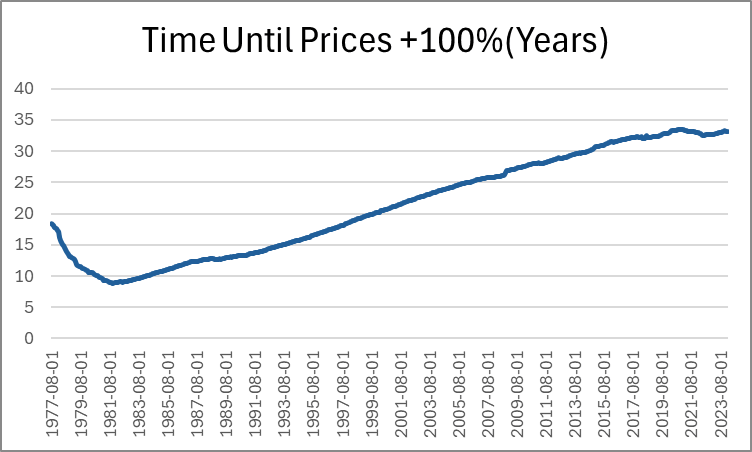Economics as a discipline really likes to boil things down to their essentials. There are plenty of examples. How many goods can one consume? Just two, bread and not bread. How can you spend your time? You can labor or leisure. How do you spend your money? Consume or save. It’s this last one that I want to emphasize here.

First, all income ultimately ends up being spent on consumption. Saving today is just the decision to consume in the future. And if not by you, then by your heirs. One determinant of inter-temporal consumption decisions is the real rate of return. That is, how many apples can you eat in the future by forgoing an apple eaten today? The bigger that number is, the more attractive the decision to save.

Further, since most saving is not in the form of cash and is instead invested in productive assets, we can also characterize the intertemporal consumption problem as the current budget allocation decision to consume or invest. The more attractive capital becomes, the more one is willing to invest rather than consume. The relative attractiveness between consumption and investment informs the consumption decision.

How attractive is investment? I’ll illustrate in two graphs. First, if the price of investment goods falls relative to consumption goods, then individuals will invest more. The graph below charts the price ratio of investment goods to consumption goods. Relative to consumption, the price of investment has fallen since 1980. Saving for the future has never been cheaper!

https://fred.stlouisfed.org/graph/?g=1p0C7

Of course, as in a price taker story, I am assuming that individuals don’t affect this price ratio. Truly, prices are endogenous to consumption/investment decisions. For all we know, it may be that the prices of investment goods are falling because demand for investment goods has fallen. But that doesn’t appear to be the case.

Continue reading →

Corporate Landlords Make Rent… Lower?

June 7, 2024June 7, 2024Zachary Bartsch6 Comments

Let’s keep it brief. Stick with me.

You know how perfect diversification means that one bears no idiosyncratic risk? That means that one is willing to pay more for some given return, driving up the price of assets included in such a diversified portfolio. That means that, without an informational advantage, index funds should place upward pressure on the price of assets that compose them. Anyone who invests in individual stocks, again without an informational advantage, would be priced out of the market because they bear idiosyncratic risk and would need to enjoy a risk premium that lowers the maximum price that they are willing to pay.

What about real estate?

Continue reading →

Taxes & Unemployment – Know Your Bias?

May 30, 2024May 31, 2024Zachary Bartsch2 Comments

Say that there is a labor market and that there is no income tax. If an income tax is introduced, then what should we expect to happen? Specifically, what will happen to employment, the size of the labor force, and the number of people unemployed? Will each rise? Fall? Remain unchanged? Change ambiguously? Take a moment and jot down a note to test yourself.

As it turns out, what your answer is depends on what your model of the labor market is. Graphically, they are all quantities of labor. The size of the labor force is the quantity of labor supplied contingent on some wage that workers receive. It’s the number of people who are willing to work. Employment is the quantity of laborers demanded by firms contingent on to wage that they pay. Finally, the quantity of people unemployed is the difference between the size of the labor force and the quantity of workers employed (Assuming that the labor force is greater than or equal to employment).

Continue reading →

Hotel Taxes and Quality: Why Georgia Sucks (Value)

May 24, 2024Zachary Bartsch4 Comments

Every year my family travels from SW Florida to the mid Atlantic area. Without stops it takes 16-17 hours. With small children, it’s definitely a two day trip. We find that they handle it better if we leave super early, take a longer leg on the first day, then stop at a hotel midway and get the kids in the pool to help burn off some energy. We also rent a suite whenever possible.

We’ve made this trip many times. I use the Bonvoy app which is for Marriott hotels. We even have a particular hotel that we prefer: The Fairfield Inn in Santee, SC. It’s clean, spacious, the employees are welcoming and kind, the breakfast includes cooked items that aren’t bad, it’s within walking distance of a grocery store, and the price isn’t bad at all. Fairfield Inns are generally a great price per quality…. But not in Georgia.

I’ve stopped at several Fairfield Inns in GA: near Atlanta, near Savannah, and we’ve been disappointed. Every. Single. Time. All the margins on which the Fairfield in Santee is great are the same margins on which Georgia ones are poor. I’m sure that there is not just one reason. Maybe there is a bad regional manager or bad assistant to the regional manager. That’s not my primary hypothesis though.

Continue reading →

Almost Observable Human Capital

May 17, 2024May 17, 2024Zachary BartschLeave a comment

I’ve written about IPUMS before. It’s great. Among individual details are their occupations and industry of their occupation. That’s convenient because we can observe how technology spread across America by observing employment in those industries. We can also identify whether demographic subgroups differed or not by occupation. There’s plenty of ways to slice the data: sex, race, age, nativity, etc.

But what do we know about historical occupations and what they entailed? At first blush, we just have our intuition. But it turns out that we have more. There is a super boring 1949 report published by the Department of Labor called the “Dictionary of Occupational Titles”. The title says it all. But, the DOL published another report in 1956 that’s conceptually more interesting called “Estimates of Worker Trait Requirements for 4,000 Jobs as Defined in the Dictionary of Occupational Titles: An Alphabetical Index”. The report lists thousands of occupations and identifies typical worker aptitudes, worker temperaments, worker interests, worker physical capacities, and working conditions. Below is a sample of the how the table is organized:

Continue reading →

Not Crazy: Insurance Premiums

May 10, 2024May 10, 2024Zachary Bartsch4 Comments

Higher homeowner’s insurance premiums have been in the news. But are we just hearing about the extreme cases? This post is inspired by the FRED Blog post about property and casualty (P&C) insurance premium producer price indices. I dive a little deeper.

The insurance premium data is composed of seven components: